Cálculo de un iluminador de guía de onda circular
por Luis -EA4BGH-
Ecuaciones implicadas:
| Velocidad de la luz en el vacío | c = 299.792.458 | m/s (1) |
| Longitud de onda en espacio abierto | λ = c/f | m |
| Frecuencia de corte TE11 | fc = (c γ11) / (π D) | Hz |
| Frecuencia de corte TM01 | fh = (c γ01) / (π D) | Hz |
| Longitud de onda en la guía | λg = c / sqr( f<size=-1>2 - fc<size=-1>2 ) | m |
| Ancho del haz a -3 dB | BW = (180λ/ πD) | ° |
| Ganancia teórica | G = 10 log(πD / λ)<size=-1>2 | dBi |
Ejemplo práctico
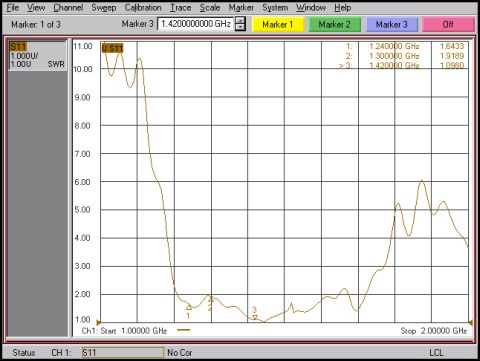
Se ha construído una antena con esta calculadora para 1,42 GHz con una lata de tomate de 5 Kg. El tamaño es estándar de la industria alimentaria, con un diámetro de 152 mm.
La ROE es menor de 2 desde 1.200 hasta 1.600 MHz, estando el mínimo en 1.440 MHz.
Teoría de funcionamiento:
Debido a la reflexión de la onda en las paredes, dentro de una guía de onda no existe un único modo de propagación como ocurre en el espacio abierto o en un cable(2). Estos modos pueden ser TE (Transversal Eléctrico) y TM (Transversal Magnético). Los modos de propagación que la guía admite dependen simplemente de sus dimensiones, digamos que depende de que la longitud de onda "quepa" en la guía. Por ello, cada modo de propagación tiene una frecuencia de corte por debajo de la cual no opera.
Se pretende operar en monomodo. En el caso de la guía de onda circular, el modo dominante es TE11, por lo que habrá que elegir un diámetro para que la frecuencia de operación se encuentre por encima de la frecuencia de corte para TE11 pero por debajo de la de TM01, que es el siguiente modo.
Las reflexiones en las paredes hacen también que la velocidad de propagación de la onda se reduzca dentro de la guía. Esto hace que λg sea mayor que λ.
A cada λg/4 de distancia desde el radiador se suceden un punto de mínima intensidad de campo y otro de máxima. Por ello, el fondo de la cavidad se coloca a λg/4 y la boca a 2 (λg/4).
NOTAS:
(1) Si la guía no está rellena de aire, se sustituirá c por υ
siendo υ=c/sqr(εr), donde εr es la constante diélectrica de la sustancia
(2) En un cable coaxial, a altas frecuencias se pueden dar los modos TE o TM. El límite de funcionamiento de TEM en monomodo se calcula por
fc no-TEM= ( 2υ ) / ( π (do+di) )siendo do, el diámetro interno de la malla y di el diámetro externo del vivo.
La frecuencia de corte del modo TEM es cero.
fc TEM= 0